The Mathematics of Noise
Authors: Miranda Zachopoulou, Daniel Dippold
What is Noise?
“Wherever there is judgment, there is noise — and more of it than you think” — Daniel Kahneman
To most people, noise is a loud or unpleasant sound that causes disturbance. In their book “Noise: A Flaw in Human Judgment”, Daniel Kahneman, Cass Sunstein and Olivier Sibony expand the statistical definition of noise and define it as the unwanted variability in professional judgments.
Often, variability in data is creating much more harm than bias. The book Noise is about this phenomenon: Whenever variability creates trouble, it usually remains undiscovered. Different judges make different judgements, sometimes to such an extreme extent that decisions from judges on jail time differ between zero and seven years. Moreover, in underwriting, hiring, and private equity, noisy decision making often costs organisations large quantities of money.
In their book, the authors refer to a noise audit; a process that helps organisations measure their level of noise. Often, this is the job of data scientists who leverage their knowledge of programming and statistics to discover when variability is creating harm. Unfortunately, Kahneman, Sunstein and Sibony never explain their statistically correct formula in detail. When we tried to implement it in practice, we realised that it was not as easy to apply without understanding the derivation of each term and how they are related to each other. Our goal with this article is to save you time and provide you with a step by step guide to performing noise audits from a technical perspective.
We want to shed light on the mathematics and technical coding implication of the noise audit to make it readily available to the data science community.
Introduction to the Different Forms of Noise
Often, we would assume that the reason for faulty judge decisions is bias. Two judges will provide different sentences for the same defendant because one judge is biased against women. However, this is not necessarily the case.
What if the judge’s favourite football team lost the night before? What if they had a fight with their partner the morning before a trial? What if they generally have a stricter personality than the average judge? What if they woke up this morning with a particularly bad headache? All these are sources of noise which can ultimately affect someone’s decision.
In their book, Kahneman, Sunstein and Sibony refer to the above examples as system noise, ie. variability within a system of judgments. This is then decomposed into:
Level Noise: The variability of an individual’s average judgement ie. is a person harsher or more lenient on average?
Pattern Noise: Variations due to individuals’ specific responses to cases/people ie.a generally harsh judge being unusually lenient with older defendants who shoplift. Pattern Noise is particularly interesting as it reflects the values, preferences, and tastes of individuals.
The relationship between the three types of noise is then presented to be:

The purpose of this article is firstly to explore the mathematical meaning of noise as presented in the book by proving the above equation, and secondly to provide an algorithm that can identify noise within a given dataset and decompose it into the two levels of noise presented.
In order to tackle the problem of noise, Kahneman, Sunstein and Sibony propose performing noise audits: giving the same task to multiple individuals within your organization and analyzing the results. The code that we have provided at the end of the article should help you perform this task — all you need to do from your side is collect the data.
To give you a spherical understanding of system noise decomposition we will examine this concept in 3 different ways:
- Understanding — the intuition behind noise
- Proving — system noise decomposition mathematically
- Coding — an algorithm that performs the decomposition automatically
Understanding
Let’s consider an example similar to the one given in the book: We are examining the noise within a judicial system with 5 cases and 10 judges. The entries in the following table are completely randomized and represent the sentences given to 5 cases by 10 judges.
It is important to note that in the book, error is defined as a deviation from the average. In statistics we refer to this as the standard deviation. Therefore, the squared errors in the formula represent the variances.

System variance (=system noise squared) is easy to obtain, as it is simply the average of the column variances, ie. 7.81.
Similarly, level variance is the variance of the row (judge) means, which is equal to 0.93.
Pattern variance is a bit more complicated to calculate, so let’s focus on the yellow highlighted cell.
Judge 1 has sentenced the criminal to 4 years in jail. The average for that particular case was 6.1 years (case A mean). The judge has given an average sentence of 5 years which is 0.7 less than the overall average of the dataset (5.7). Therefore we would expect Judge 1 to sentence criminal A to 6.1–0.7=5.4 yrs in jail. This is what would happen if there was only level noise but no pattern noise, ie. criminals would receive the mean sentence for their case minus the deviation of the judge’s mean sentence from the overall mean. The results of this calculation are shown in the green table below:

However, looking back at the given sentence in the blue table we see that the judge was more lenient than he usually is and sentenced the criminal to only 4 years in jail. The difference 5.4–4=1.4 is the pattern error, and is shown below:

To calculate the overall pattern variance, we need to calculate the average of the column variances (6.88).
We can very easily check that the system noise equation holds as 7.81 = 0.93 + 6.88.
Now that we have understood the intuition behind system noise decomposition, it is time to prove it mathematically.
Proving
The focus of the following section is to mathematically prove the system noise decomposition before implementing it algorithmically in R.
Firstly we define the following (n x m) matrix:

Using the matrix above we can create expressions for the overall mean (μ) of the matrix as well as the means of the j-th column (μj) and ith-row (μi):

Next we create expressions for the three levels of noise:
System noise² is the variability in a system the judgements which are the sentences for the different cases in this example. Therefore to calculate the overall system noise we need to take the average of the column variances:

Level Noise² is the variability in row means ie. the variability in the average sentences given by each judge.

Pattern Noise squared is the average of the variances of the differences between actual and expected differences (let’s break this one down).
We are calculating an average, therefore we automatically know that we are taking the sum of m terms and dividing by the total number of values (m since we are looking at column sums and we have m columns).
We are calculating the average of variances, therefore we need to use the typical variance formula ie (1/n)Σ(x_i-μ)². In this case our x is the difference between our actual and expected value. The mean, on the other hand, is actually zero. This is clearly shown in the orange table above, where the column sums are all equal to zero. Therefore, the only term inside the variance formula is the difference between the actual and expected values.
Recall that our actual value is x_ij while our expected value is the case mean (μ_j) minus the difference of the judge mean (μ_i) from the overall mean (μ). This leads to the following expression:

We are now ready to prove that System Noise² = Level Noise² + Pattern Noise²:

Using the difference of squares property that

and the double summation property that
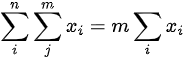
we arrive at the result above. It is now easy to prove that the 2nd and 3rd terms on the right hand side of the equation cancel out to 0, thus making the equality hold:

Simplifying each individual term from left to right:
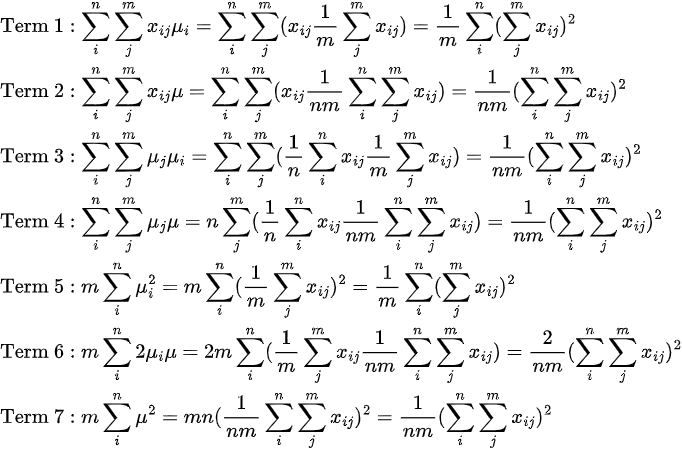
The above simplifications are all based on the fact that

This is because for every i, Σj(x_ij) becomes a constant, so by using sigma summation rules we can take it outside the j-summation thus getting

Similarly,
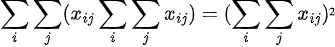
We therefore get:


Coding
Using the above noise expressions, we can now create three functions that, given any dataset, can calculate system noise and decompose it into level and pattern noise.
Firstly, we are creating the dummy matrix presented above that will be used to test our functions. The columns represent the different ‘cases’ while the rows represent the ‘judges’.
Conclusion
We hope that this article helps you with the intuition, mathematics, and code to perform a noise audit. No matter if you are a data scientist or not, we hope that we were able to sharpen your understanding of the concept of noise and raise your confidence that noise can be measured, calculated, and finally tackled.
We are very open to comments and criticism to improve this article even further. Feel free to engage, reach out, and discuss the concept of noise with us. At NEWNOW, we deeply believe in the value of data science, statistics, and machine learning and hope that we play a small role within the wider movement of using noise audits to increase fairness and reduce costs.
